Ребенок обладает всеми интуитивными знаниями, необходимыми для подготовки к абстрактным идеям счета. Понятие количества было присуще всем нашим материалам, предназначенным для воспитания чувств: например, они могли быть длиннее и короче, темнее и светлее. Понятия сходства и различия были частью техники воспитания чувств, которая началась с распознавания одинаковых предметов и продолжилась ступенчатой расстановкой похожих предметов. Приведу для примера первое упражнение с цилиндрами, которое может делать ребенок даже двух с половиной лет. Когда он делает ошибку, вставляя цилиндр в слишком большое углубление и таким образом оставляя один цилиндр без места, он интуитивно понимает, что один предмет выбивается из общей серии.
Ум ребенка нельзя подготовить к идее числа с помощью каких-то «вводных понятий», которые поспешно объясняются учителем. Это возможно только с помощью процесса формирования, медленного самовыстраивания логической цепочки.
Чтобы перейти непосредственно к обучению арифметике, мы возвращаемся к тому же дидактическому материалу, который использовали для развития сенсорики.
Давайте взглянем на три набора предметов, которые были представлены после упражнений с геометрическими фигурами-вставками, то есть материал для обучения понятию размера (розовые кубы), толщины (коричневые призмы) и длины (зеленые планки). В материале, обучающем понятию длины, самый короткий предмет является единицей измерения для всех остальных. Второй предмет вдвое больше первого, третий в три раза больше первого и т. д. Таким образом, длина увеличивается от предмета к предмету каждый раз на 10 см, остальные параметры остаются постоянными (например, всех планки имеют одинаковые сечения).
Поэтому предметы находятся в той же зависимости друг от друга, как и простой натуральный ряд чисел 1, 2, 3, 4, 5, 6, 7, 8, 9, 10.
Во втором наборе, то есть в том, который демонстрирует толщину, длина остается постоянной, а площадь основания призмы – разная. В результате сторона основания изменяется в соответствии с рядом натуральных чисел, например, у первой призмы основание имеет стороны по 1 см, во втором – 2 см, в третьем – 3 см и т. д. вплоть до десятой призмы, у которой сторона основания – 10 см. Таким образом, призмы относятся друг к другу как ряд квадратов натуральных чисел (1, 4, 9, 16 и т. д.), так как надо взять четыре призмы первого размера, чтобы получить вторую, девять, чтобы получить третью, и т. д. Поэтому предметы, входящие в набор, обучающий понятию толщины, находятся в следующем соотношении: 1: 4: 9: 16: 25: 36: 49: 64: 81: 100.
В случае с розовыми кубиками их грани увеличиваются в соответствии с натуральным рядом чисел. То есть первый кубик имеет грань размером 1 см, второй – 2 см, третий – 3 см и так далее до десятого куба, грань которого равна 10 см. Поэтому соотношение их объемов такое же, как и ряд величин третьей степени чисел от 1 до 10, то есть 1: 8: 27: 64: 125: 216: 343: 512: 729: 1000. Ведь чтобы получить объем второго розового куба, понадобится восемь маленьких первых кубов. А чтобы получить третий куб, понадобится двадцать семь вторых и т. д.
Дети обладают интуитивным пониманием этой разницы, так как они знают, что упражнение с розовыми кубиками – самое легкое из этих трех, а с планками – самое сложное. Чтобы приступить к непосредственному изучению чисел, нам понадобятся длинные планки, но теперь мы видоизменяем их, разделяя на десять равных частей: каждая имеет по 10 см в длину и выкрашена полосами в красный и синий цвет. Например, сразу будет видно, что планка, которая в четыре раза больше первой, поделена на четыре равные части, красные и синие, и точно так же будут выглядеть все остальные.
Разложив планки по степени возрастания их длины, мы показываем детям числа: 1, 2, 3 и т. д., дотрагиваясь до планок по порядку, от первой до десятой. Затем, чтобы помочь ребенку получить ясное представление о числе, мы продолжаем учиться различать отдельные планки с помощью обычных трех этапов.
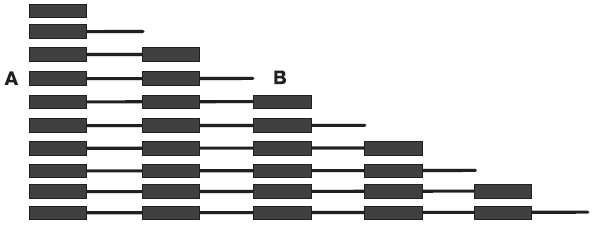

Рис. 28. Схема, иллюстрирующая использование планок для изучения цифр
Мы выкладываем перед ребенком первые три планки и, показывая на них или беря в руку по очереди, говорим: «Это – один. Это – два. Это – три». Мы показываем пальцем на деления на каждой планке и пересчитываем их так, чтобы убедиться: «Один, два: это два. Один, два, три: это три». Затем мы говорим ребенку: «Дай мне два. Дай мне один. Дай мне три». Наконец, указывая на планку, спрашиваем: «Что это?» Точно так же мы показываем детям все остальные планки по порядку, добавляя каждый раз одну или две, в зависимости от способностей ребенка.
Важность этого дидактического материала состоит в том, что он дает ясное представление о числе. Потому что, когда число получает свое название, оно существует как самостоятельный предмет, целое. Когда мы говорим, что у человека есть миллион, мы имеем в виду, что у него есть состояние, которое состоит из большого количества единиц ценностей. И все эти единицы принадлежат одному человеку.
Так, если складывать 7 и 8 (7+8), мы добавляем число к числу, и эти числа по четко установленным правилам представляют собой группы однородных единиц.
Опять же, когда ребенок показывает нам цифру 9, он держит в руке единую планку – целый предмет, состоящий из девяти одинаковых частей, которые можно сосчитать. И потом, когда ему нужно будет прибавить 8 к 2, он положит рядом две планки, два предмета, один из которых состоит из восьми одинаковых частей, а другой из двух.
С другой стороны, в обычных школах, чтобы детям было легче научиться считать, им предлагают считать разные предметы, например бобы, палочки и т. д. Если, взяв пример, о котором я говорила (8+2), ребенок берет восемь палочек и прибавляет к ним еще две, естественное впечатление, которое складывается у него голове, – не то, что он добавил 8 к 2, а то, что он сложил 1 + 1+1 + 1 + 1+1 + 1+1 и 1 + 1. Результат не такой наглядный, и ребенку нужно приложить усилия, удерживая в голове мысль о том, что группа из восьми предметов – это единое целое, соответствующее одной общей цифре, 8.
Это усилие часто задерживает ребенка, замедляет его понимание чисел на месяцы или даже годы.
Сложение и вычитание чисел до 10 тоже будет даваться ребенку намного быстрее, если использовать дидактический материал для изучения длины. Предложите ребенку интересную задачу – как выложить предметы так, чтобы получился набор планок, по длине равных самой длинной из них. Сначала он расставляет планки в их правильном порядке по убыванию (длинной лесенкой). Затем он берет последнюю планку (1) и кладет ее рядом с 9. Затем он берет планку, следующую за первой (2), и кладет ее рядом с 8 и так далее до 5.
Эта очень простая игра демонстрирует сложение чисел до десяти: 9+1, 8+2, 7+3, 6+4. Затем, когда ребенок раскладывает планки назад на свои места, он должен сначала убрать 4 и положить ее назад рядом с 5, потом убрать в свою очередь 3, 2, 1. Таким образом, он снова раскладывает планки в их правильной последовательности и одновременно выполняет вычитания 10 – 4, 10 – 3, 10 – 2, 10 – 1.
Изучение цифр характеризует переход от планок к счету различных предметов. Когда цифры уже известны, они начинают служить той самой абстрактной цели, которую планки воплощают конкретно. Таким образом, цифры займут место планок для того, чтобы объединять в единое целое некоторое количество отдельных единиц. Синтетическая функция языка и широкое поле, которое язык открывает для интеллектуальной работы, проявляется в том, что можно было бы назвать функцией цифры, которая в данный момент заменяется конкретными планками.
Использование этих планок ограничит знания арифметики только несложными вычислениями в пределах десяти или чуть дальше. Эти вычисления лишь ненамного продвинут вперед развитие разума, выйдя за пределы, заданные первыми простыми упражнениями на воспитание чувств. Именно цифра, которая, как и буква, является графическим символом, может дать толчок тому бесконечному движению вперед, которое проделал математический разум человека.
Среди дидактического материала есть коробка, содержащая гладкие карточки, на которые наклеены вырезанные из шероховатой бумаги цифры – от одного до девяти. Эти карточки похожи на те, на которые наклеены шероховатые буквы алфавита. И метод их изучения точно такой же. Ребенок проводит пальцами по шероховатой поверхности цифр, чтобы понять, как они пишутся, и одновременно с этим произносит их название. Однако в данном случае ребенок делает больше, чем тогда, когда учил буквы. Он будет учиться раскладывать цифры на соответствующие им планки.
Когда ребенок выучит все цифры, он приступает к первому упражнению. Нужно разложить карточки на планки, выстроенные в порядке возрастания. Собранные таким образом планки выглядят как лесенка, на которую очень удобно раскладывать карточки. И ребенок может очень долго сидеть, повторяя эту умную игру.
После этого начинается то, что мы называем самостоятельностью ребенка. Он носит свои цифры с собой и, используя их, может теперь раскладывать предметы по группам. Для этой цели в нашем дидактическом материале есть набор деревянных палочек. А в дополнение к ним мы даем ребенку разного рода маленькие предметы – маленькие кубики, фишки и т. д.
Упражнение состоит в том, чтобы класть напротив цифры соответствующее ей количество предметов. Ребенок для этого может использовать коробку, входящую в дидактический материал. Коробка разделена на отделения, на каждом из которых написана цифра. В каждую ячейку нужно положить соответствующее ей число палочек.
Другое упражнение состоит в том, чтобы выкладывать на стол карточки с цифрами, а на них – соответствующее число кубиков, фишек и т. д.
И это только первый шаг. Здесь у меня нет возможности рассказывать подробно об успешных уроках обучения детей нулю, десяткам и другим арифметическим действиям – для этого обращайтесь к другим моим работам. Но сам по себе дидактический материал уже может подсказать вам идеи. В коробке, в которой лежат палочки, есть отделение, на котором нарисован 0. Внутри этого отделения ничего не нужно класть, а затем мы начинаем с единицы.
Ноль – это ничего, но его нужно расположить рядом с единицей, чтобы после 9 мы могли перейти к 10.
Если бы, вместо планки 1, мы взяли бы за единицу отсчета планку 10, мы могли бы считать 10, 20, 30, 40, 50, 60, 70, 80, 90. Среди дидактического материала есть рамки, к которым приделаны карточки с числами от 10 до 90. Эти числа закреплены таким образом, чтобы цифры от 1 до 9 могли бы на них надвигаться сверху, закрывая ноль. Таким образом, если ноль в цифре 10 закрыть единицей, получится 11, а если двойкой – то получится 12 и так далее до 9. Потом мы переходим к двадцаткам (второй десяток) и так далее, от десятки к десятке (рис. 29).

Рис. 29
Для того чтобы приступить к упражнению с карточками, на которых нарисованы десятки, мы можем использовать планки. Так как мы начинаем с первой десятки (10) в рамке, мы берем планку 10. Затем кладем маленькую планку 1 рядом с планкой 10 и в то же время двигаем в рамке цифру 1, закрывая ноль в цифре 10. Затем мы убираем планку 1 и цифру 1 с рамки и кладем на их место планку 2 рядом с планкой 10, а цифру 2 надвигаем поверх ноля в рамке. И так до 9. Для продолжения нам понадобятся две планки по 10, чтобы получилось 20.
Дети с большим энтузиазмом выполняют эти упражнения, которые требуют от них двойных усилий и в то же время помогают ясно представить эти понятия.
Обучаясь письму и арифметике, дети пожинают плоды трудоемкого воспитания, которое состояло из того, чтобы научиться координировать свои движения и получить первые знания о мире. Эти достижения приходят как естественный результат первых попыток человека начать интеллектуальный взаимообмен с внешним миром.
Все эти первые открытия, которые выстроились в сознании ребенка в целостную систему, могут утратиться, если не будут надежно закреплены благодаря письменному языку и цифрам. Однако полученный таким образом опыт открывает неограниченные возможности и для дальнейшего обучения. Поэтому мы должны подвести ребенка к более высокой ступени – к совершенствованию, после чего он сможет пойти в школу. Но не в традиционную школу, известную нам сейчас, где мы абсолютно нелогично пытаемся давать знания еще не подготовленным умам, которые не были воспитаны, чтобы получать их.
Чтобы сохранить здоровый образ мыслей, чтобы разум упражнялся, но не был изнурен порядком работы, наши дети должны получить новый вид школы для продолжения в ней необходимого образования. А я также продолжаю расширять мой метод и дальше, для детей старшего возраста.
Ум ребенка нельзя подготовить к идее числа с помощью каких-то «вводных понятий», которые поспешно объясняются учителем. Это возможно только с помощью процесса формирования, медленного самовыстраивания логической цепочки.
Чтобы перейти непосредственно к обучению арифметике, мы возвращаемся к тому же дидактическому материалу, который использовали для развития сенсорики.
Давайте взглянем на три набора предметов, которые были представлены после упражнений с геометрическими фигурами-вставками, то есть материал для обучения понятию размера (розовые кубы), толщины (коричневые призмы) и длины (зеленые планки). В материале, обучающем понятию длины, самый короткий предмет является единицей измерения для всех остальных. Второй предмет вдвое больше первого, третий в три раза больше первого и т. д. Таким образом, длина увеличивается от предмета к предмету каждый раз на 10 см, остальные параметры остаются постоянными (например, всех планки имеют одинаковые сечения).
Поэтому предметы находятся в той же зависимости друг от друга, как и простой натуральный ряд чисел 1, 2, 3, 4, 5, 6, 7, 8, 9, 10.
Во втором наборе, то есть в том, который демонстрирует толщину, длина остается постоянной, а площадь основания призмы – разная. В результате сторона основания изменяется в соответствии с рядом натуральных чисел, например, у первой призмы основание имеет стороны по 1 см, во втором – 2 см, в третьем – 3 см и т. д. вплоть до десятой призмы, у которой сторона основания – 10 см. Таким образом, призмы относятся друг к другу как ряд квадратов натуральных чисел (1, 4, 9, 16 и т. д.), так как надо взять четыре призмы первого размера, чтобы получить вторую, девять, чтобы получить третью, и т. д. Поэтому предметы, входящие в набор, обучающий понятию толщины, находятся в следующем соотношении: 1: 4: 9: 16: 25: 36: 49: 64: 81: 100.
В случае с розовыми кубиками их грани увеличиваются в соответствии с натуральным рядом чисел. То есть первый кубик имеет грань размером 1 см, второй – 2 см, третий – 3 см и так далее до десятого куба, грань которого равна 10 см. Поэтому соотношение их объемов такое же, как и ряд величин третьей степени чисел от 1 до 10, то есть 1: 8: 27: 64: 125: 216: 343: 512: 729: 1000. Ведь чтобы получить объем второго розового куба, понадобится восемь маленьких первых кубов. А чтобы получить третий куб, понадобится двадцать семь вторых и т. д.
Дети обладают интуитивным пониманием этой разницы, так как они знают, что упражнение с розовыми кубиками – самое легкое из этих трех, а с планками – самое сложное. Чтобы приступить к непосредственному изучению чисел, нам понадобятся длинные планки, но теперь мы видоизменяем их, разделяя на десять равных частей: каждая имеет по 10 см в длину и выкрашена полосами в красный и синий цвет. Например, сразу будет видно, что планка, которая в четыре раза больше первой, поделена на четыре равные части, красные и синие, и точно так же будут выглядеть все остальные.
Разложив планки по степени возрастания их длины, мы показываем детям числа: 1, 2, 3 и т. д., дотрагиваясь до планок по порядку, от первой до десятой. Затем, чтобы помочь ребенку получить ясное представление о числе, мы продолжаем учиться различать отдельные планки с помощью обычных трех этапов.


Рис. 28. Схема, иллюстрирующая использование планок для изучения цифр
Мы выкладываем перед ребенком первые три планки и, показывая на них или беря в руку по очереди, говорим: «Это – один. Это – два. Это – три». Мы показываем пальцем на деления на каждой планке и пересчитываем их так, чтобы убедиться: «Один, два: это два. Один, два, три: это три». Затем мы говорим ребенку: «Дай мне два. Дай мне один. Дай мне три». Наконец, указывая на планку, спрашиваем: «Что это?» Точно так же мы показываем детям все остальные планки по порядку, добавляя каждый раз одну или две, в зависимости от способностей ребенка.
Важность этого дидактического материала состоит в том, что он дает ясное представление о числе. Потому что, когда число получает свое название, оно существует как самостоятельный предмет, целое. Когда мы говорим, что у человека есть миллион, мы имеем в виду, что у него есть состояние, которое состоит из большого количества единиц ценностей. И все эти единицы принадлежат одному человеку.
Так, если складывать 7 и 8 (7+8), мы добавляем число к числу, и эти числа по четко установленным правилам представляют собой группы однородных единиц.
Опять же, когда ребенок показывает нам цифру 9, он держит в руке единую планку – целый предмет, состоящий из девяти одинаковых частей, которые можно сосчитать. И потом, когда ему нужно будет прибавить 8 к 2, он положит рядом две планки, два предмета, один из которых состоит из восьми одинаковых частей, а другой из двух.
С другой стороны, в обычных школах, чтобы детям было легче научиться считать, им предлагают считать разные предметы, например бобы, палочки и т. д. Если, взяв пример, о котором я говорила (8+2), ребенок берет восемь палочек и прибавляет к ним еще две, естественное впечатление, которое складывается у него голове, – не то, что он добавил 8 к 2, а то, что он сложил 1 + 1+1 + 1 + 1+1 + 1+1 и 1 + 1. Результат не такой наглядный, и ребенку нужно приложить усилия, удерживая в голове мысль о том, что группа из восьми предметов – это единое целое, соответствующее одной общей цифре, 8.
Это усилие часто задерживает ребенка, замедляет его понимание чисел на месяцы или даже годы.
Сложение и вычитание чисел до 10 тоже будет даваться ребенку намного быстрее, если использовать дидактический материал для изучения длины. Предложите ребенку интересную задачу – как выложить предметы так, чтобы получился набор планок, по длине равных самой длинной из них. Сначала он расставляет планки в их правильном порядке по убыванию (длинной лесенкой). Затем он берет последнюю планку (1) и кладет ее рядом с 9. Затем он берет планку, следующую за первой (2), и кладет ее рядом с 8 и так далее до 5.
Эта очень простая игра демонстрирует сложение чисел до десяти: 9+1, 8+2, 7+3, 6+4. Затем, когда ребенок раскладывает планки назад на свои места, он должен сначала убрать 4 и положить ее назад рядом с 5, потом убрать в свою очередь 3, 2, 1. Таким образом, он снова раскладывает планки в их правильной последовательности и одновременно выполняет вычитания 10 – 4, 10 – 3, 10 – 2, 10 – 1.
Изучение цифр характеризует переход от планок к счету различных предметов. Когда цифры уже известны, они начинают служить той самой абстрактной цели, которую планки воплощают конкретно. Таким образом, цифры займут место планок для того, чтобы объединять в единое целое некоторое количество отдельных единиц. Синтетическая функция языка и широкое поле, которое язык открывает для интеллектуальной работы, проявляется в том, что можно было бы назвать функцией цифры, которая в данный момент заменяется конкретными планками.
Использование этих планок ограничит знания арифметики только несложными вычислениями в пределах десяти или чуть дальше. Эти вычисления лишь ненамного продвинут вперед развитие разума, выйдя за пределы, заданные первыми простыми упражнениями на воспитание чувств. Именно цифра, которая, как и буква, является графическим символом, может дать толчок тому бесконечному движению вперед, которое проделал математический разум человека.
Среди дидактического материала есть коробка, содержащая гладкие карточки, на которые наклеены вырезанные из шероховатой бумаги цифры – от одного до девяти. Эти карточки похожи на те, на которые наклеены шероховатые буквы алфавита. И метод их изучения точно такой же. Ребенок проводит пальцами по шероховатой поверхности цифр, чтобы понять, как они пишутся, и одновременно с этим произносит их название. Однако в данном случае ребенок делает больше, чем тогда, когда учил буквы. Он будет учиться раскладывать цифры на соответствующие им планки.
Когда ребенок выучит все цифры, он приступает к первому упражнению. Нужно разложить карточки на планки, выстроенные в порядке возрастания. Собранные таким образом планки выглядят как лесенка, на которую очень удобно раскладывать карточки. И ребенок может очень долго сидеть, повторяя эту умную игру.
После этого начинается то, что мы называем самостоятельностью ребенка. Он носит свои цифры с собой и, используя их, может теперь раскладывать предметы по группам. Для этой цели в нашем дидактическом материале есть набор деревянных палочек. А в дополнение к ним мы даем ребенку разного рода маленькие предметы – маленькие кубики, фишки и т. д.
Упражнение состоит в том, чтобы класть напротив цифры соответствующее ей количество предметов. Ребенок для этого может использовать коробку, входящую в дидактический материал. Коробка разделена на отделения, на каждом из которых написана цифра. В каждую ячейку нужно положить соответствующее ей число палочек.
Другое упражнение состоит в том, чтобы выкладывать на стол карточки с цифрами, а на них – соответствующее число кубиков, фишек и т. д.
И это только первый шаг. Здесь у меня нет возможности рассказывать подробно об успешных уроках обучения детей нулю, десяткам и другим арифметическим действиям – для этого обращайтесь к другим моим работам. Но сам по себе дидактический материал уже может подсказать вам идеи. В коробке, в которой лежат палочки, есть отделение, на котором нарисован 0. Внутри этого отделения ничего не нужно класть, а затем мы начинаем с единицы.
Ноль – это ничего, но его нужно расположить рядом с единицей, чтобы после 9 мы могли перейти к 10.
Если бы, вместо планки 1, мы взяли бы за единицу отсчета планку 10, мы могли бы считать 10, 20, 30, 40, 50, 60, 70, 80, 90. Среди дидактического материала есть рамки, к которым приделаны карточки с числами от 10 до 90. Эти числа закреплены таким образом, чтобы цифры от 1 до 9 могли бы на них надвигаться сверху, закрывая ноль. Таким образом, если ноль в цифре 10 закрыть единицей, получится 11, а если двойкой – то получится 12 и так далее до 9. Потом мы переходим к двадцаткам (второй десяток) и так далее, от десятки к десятке (рис. 29).

Рис. 29
Для того чтобы приступить к упражнению с карточками, на которых нарисованы десятки, мы можем использовать планки. Так как мы начинаем с первой десятки (10) в рамке, мы берем планку 10. Затем кладем маленькую планку 1 рядом с планкой 10 и в то же время двигаем в рамке цифру 1, закрывая ноль в цифре 10. Затем мы убираем планку 1 и цифру 1 с рамки и кладем на их место планку 2 рядом с планкой 10, а цифру 2 надвигаем поверх ноля в рамке. И так до 9. Для продолжения нам понадобятся две планки по 10, чтобы получилось 20.
Дети с большим энтузиазмом выполняют эти упражнения, которые требуют от них двойных усилий и в то же время помогают ясно представить эти понятия.
Обучаясь письму и арифметике, дети пожинают плоды трудоемкого воспитания, которое состояло из того, чтобы научиться координировать свои движения и получить первые знания о мире. Эти достижения приходят как естественный результат первых попыток человека начать интеллектуальный взаимообмен с внешним миром.
Все эти первые открытия, которые выстроились в сознании ребенка в целостную систему, могут утратиться, если не будут надежно закреплены благодаря письменному языку и цифрам. Однако полученный таким образом опыт открывает неограниченные возможности и для дальнейшего обучения. Поэтому мы должны подвести ребенка к более высокой ступени – к совершенствованию, после чего он сможет пойти в школу. Но не в традиционную школу, известную нам сейчас, где мы абсолютно нелогично пытаемся давать знания еще не подготовленным умам, которые не были воспитаны, чтобы получать их.
Чтобы сохранить здоровый образ мыслей, чтобы разум упражнялся, но не был изнурен порядком работы, наши дети должны получить новый вид школы для продолжения в ней необходимого образования. А я также продолжаю расширять мой метод и дальше, для детей старшего возраста.
<< Назад Вперёд>>
Просмотров: 3944







